| December 5, 2023 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
How does capacity correlate with charge voltage for lithium iron phosphate batteries? |
 3.65 Volts per cell battery chargers for
LiFePO4 packs from PowerStream. 1-cell to 8-Cell chargers.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
How much voltage does it take to charge a lithium-ion battery?Motivation: Most batteries have a distinct charge voltage. Below that voltage you cannot move the chemistry in the right direction, above that voltage you can fully charge the battery, even though it might take a long time if you are barely above the chemistry voltage.With lithium-ion (lithium-ion, lithium polymer, lithium iron phosphate, etc.) this is not the case. There is a voltage below which there is no action, the chemistry just won't move. But a big part of the charging process is getting ions in and out of solid compounds. These compounds have space between the crystal planes, or within the crystal structure, for small ions, such as lithium, to insert themselves. But it takes force to drive them in, and the more force the more the loading of the crystal. This loading of small atoms into a crystal structure is called intercalation. So it makes sense that the amount of charging depends on the voltage. But how? I haven't been able to find any data on this, so we decided to do the experiment. Method 1. I used a 26650 cells from four different manufacturers. This shows that there is some variation in the chemistry of LiFePO4 cells, but the gross features are the same. 2. Charging was done with a lab power supply, the voltage was set and the power supply current was limited to 1.6 amps. The battery would start out at 1.6 amps and when the voltage rose to the set limit, the current would drop. In most cases I waited until the current dropped to below 30mA. This is a classic constant current-constant voltage charge. 3. The battery was discharged at 2.5A rate, approximately 1C to 2.6 volts termination voltage. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Commentary. I include the lithium ion results at the very bottom of this page for comparison. As you can see the iron phosphate results also show an increase in the capacity with charge voltage, but there are some interesting differences. First, the charging starts at a lower voltage than lithium ion, with some charging starting as low as 3V. Second, there is significant charging at 3.3 volts, which opens up some applications for battery backups in 3.3 volt systems. Third, there isn't much difference in capacity when charged at 3.4V or 4.2 volts. Maybe 3% maximum. So surprisingly you can charge one of these cells at 3.4V and get almost the same capacity as charging at the recommended 3.65V. *Note: Charging above 4.20 volts is bad for the battery cycle life! 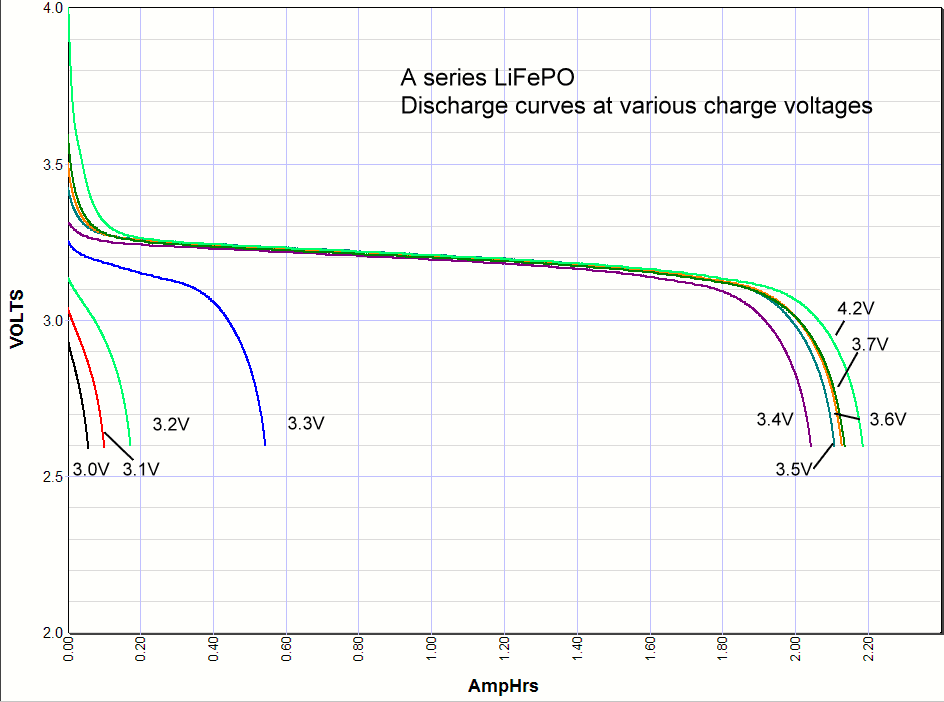 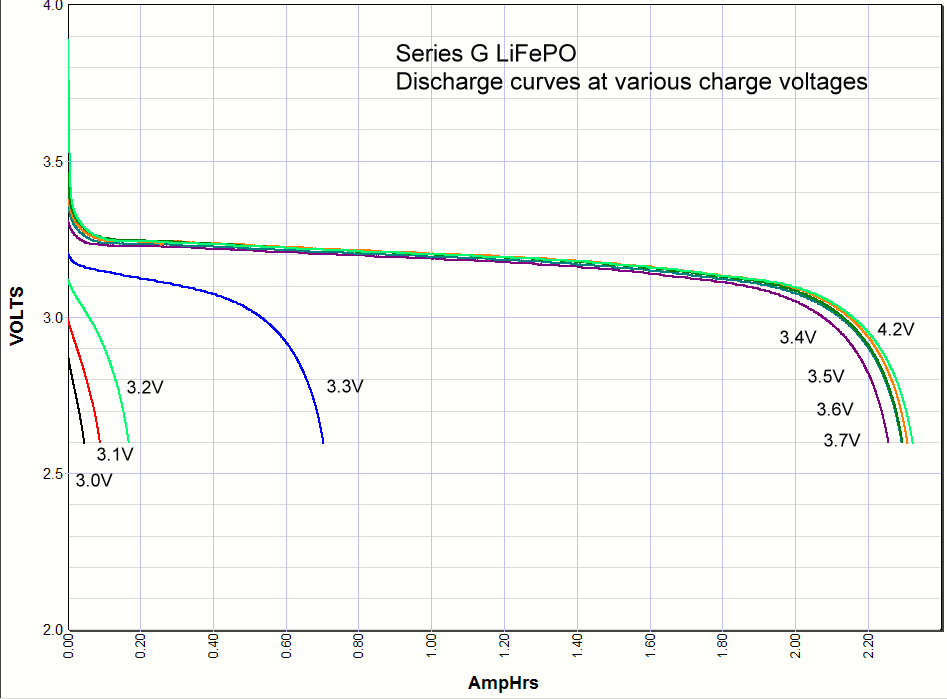 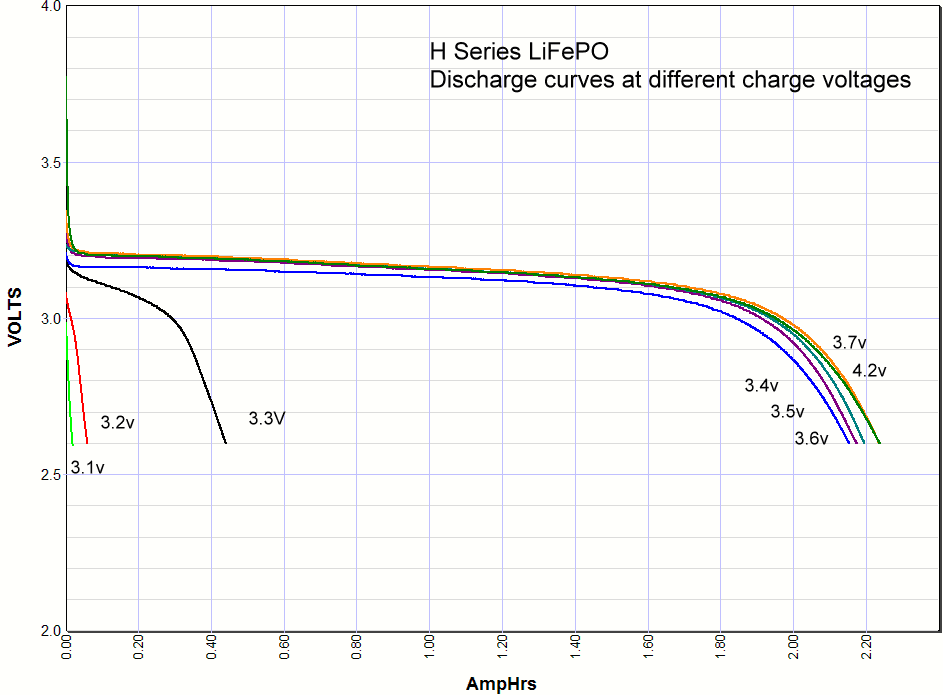 Commentary: It looks like the magic number is around
3.3 volts. Below that you don't have significant charging, above that you do. A
lithium iron phosphate battery doesn't care if it is never fully charged, so if
all you have available is 3.3 volts and you don't mind the loss in capacity you
could use the 3.3 volts. This opens up new possibility for a simple but very
long life backup battery in 3.3 volt systems.It looks like the A series cells definitely have some lithium cobalt mixed in with the iron phosphate because when it is charged to 4.2 volts there is higher voltage at the beginning of the discharge, whereas the others don't have any energy stored between 4.2V and 3.6V. You can also see this effect at the end of the discharge curve where this added capacity at the beginning of the discharge curve shows up in pushing the end of the discharge curve further out.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| |||||||||
